
Understanding the A* Search Algorithm: A 2024 Guide
Human intelligence has been the cornerstone of our progress, enabling us to create tools and technologies that enhance our lives. Artificial intelligence (AI) is a step further, designed to extend human intellect and drive unprecedented advancements in various fields. Among the powerful tools developed under AI is the A* Search Algorithm. This guide explores the A* algorithm in detail, including its principles, steps, and implementation in Python.
AI tackles complex computational challenges, such as pathfinding problems, which involve determining the best route from point A to point B. A* Search Algorithm is an efficient solution for such problems, especially when mapped to graphs where nodes represent possible outcomes. Originally developed for the Shakey project—a pioneering effort to create a mobile robot with AI—the A* algorithm has since become a versatile tool for various applications, including video games and robotics.
What is the A* Search Algorithm?
The A* Search Algorithm is distinct from other traversal methods due to its intelligence in decision-making. It’s designed to find the most efficient path by combining the best features of both informed and uninformed search algorithms.
Imagine navigating a vast maze that takes hours to complete manually. By treating this maze as a search problem, the A* algorithm can drastically reduce the time and effort needed to find a solution. It does this by evaluating each potential path based on defined criteria such as cost, distance, and direction, ensuring that only the most promising routes are explored.
Key Steps in the A* Search Algorithm
Initialize the Open List:
Start by adding the initial node to the open list.
Iterate Through Possible Paths:
Identify the square with the lowest F cost and move it to the closed list.
For each of the 8 adjacent squares, check if it’s viable. If it is, calculate the F, G, and H costs.
If a more efficient path is found, update the parent and recalculate scores.
Path Completion:
If the target is found, trace back the path from the target to the start.
If no path is found, the algorithm terminates.
Why Choose the A* Search Algorithm?
Pathfinding is complex, especially in dynamic environments. The A* algorithm excels because it proactively finds the shortest and most efficient path, unlike other algorithms that may only react to obstacles. However, A* can be slower in some cases, which is why it’s often used in combination with other algorithms for optimal performance.
A* Search Algorithm Fundamentals
A* operates using heuristic methods, which guide it toward optimal solutions. It’s a variant of the best-first search algorithm, offering both completeness (if a solution exists, it will find it) and optimality (it will find the best solution). The efficiency of A* largely depends on the quality of the heuristic function, which estimates the distance to the goal.

Implementation in Python
The A* algorithm can be implemented in Python to find the most cost-effective path in a graph. The example provided demonstrates how A* evaluates different paths and selects the optimal route based on the calculated costs.
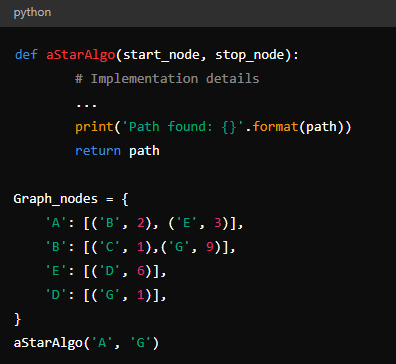
Output:
Path Found: ['A', 'E', 'D', 'G']
Frequently Asked Questions (FAQs)
A* works by exploring the graph’s vertices, starting from the initial point and examining the next vertex based on the lowest cost.
What’s the difference between A* and AO* algorithms?
A* finds a single solution, while AO* finds multiple solutions by ANDing over branches.
Why is A* popular?
A* is widely used for pathfinding and graph traversal, making it essential in games and navigation systems.
Is A* better than Dijkstra?
Yes, A* is generally better as it uses informed searches, making it more efficient.
Does Google Maps use A*?
No, Google Maps primarily uses the Dijkstra algorithm.
Why is A* considered optimal?
A* is optimal because it consistently finds the most efficient path to the goal.
How is overestimation handled in A*?
Overestimation occurs when the heuristic overestimates the actual cost, which can be adjusted by recalibrating the heuristic function.
Comments (0)